作者:何了一
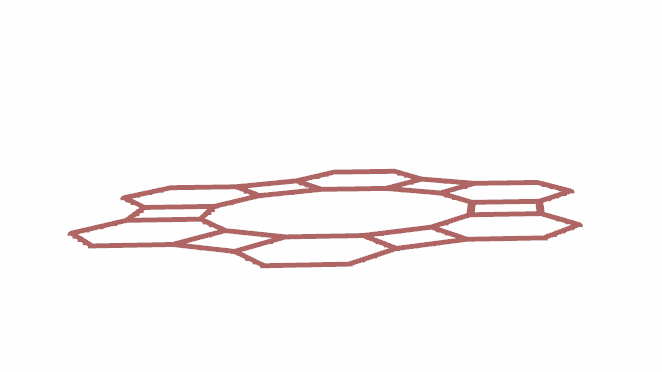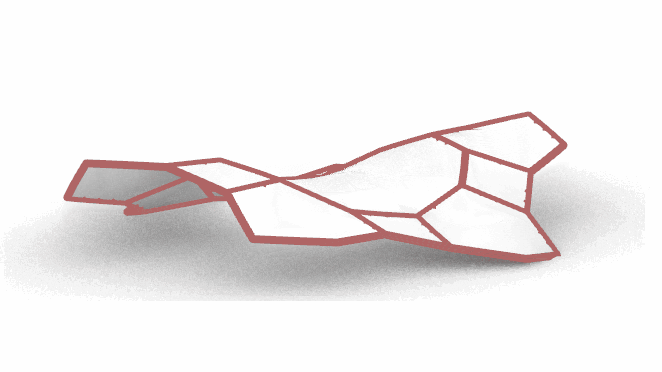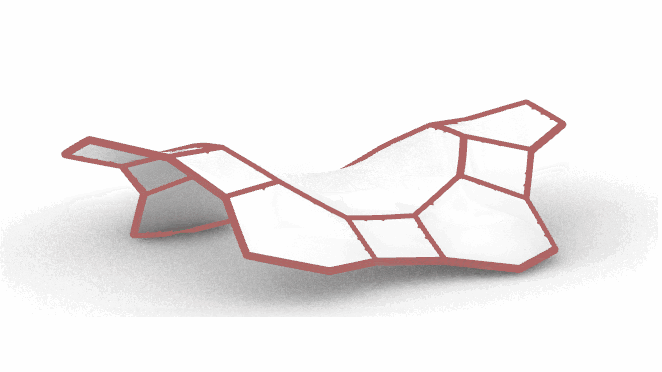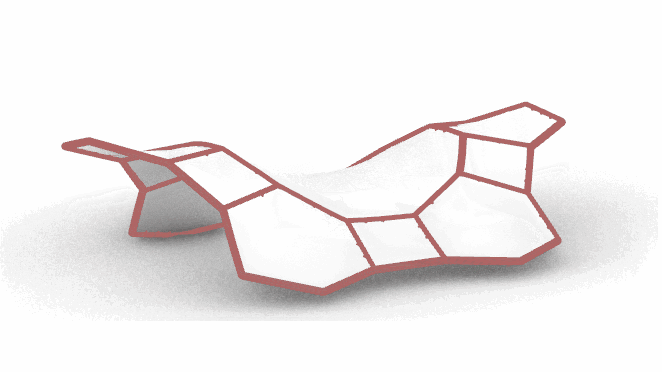
传统的3D打印技术在打印完后,物体的形状就已经定型了,这取决于3D打印都是喷嘴一层层堆叠上去的(additive manufacturing)。在学术界,有那么一小撮研究员设想,能否在3D打印完成之后改变它的形状呢?即把3D打印从3D扩展为4D,加入一个D(dimension) – “时间”的概念。实现这个目的有很多种方法,将3D打印材料打印在预拉伸弹性材料就是其中一个手段(如下图)。这个主题恰巧是笔者的研究生论文的一部分,而通过Kangaroo可以去模拟这种形变。作为Rhino原厂的Kangaroo学员之一,特意写下该文章以此答谢Rhino原厂工程师Dixon在这期间给我有限元分析方面的建议,以及献给Rhino中文社区。
1# 3D打印过程简述及力学分析
1.1 过程简述
3D打印前,纺织物被拉伸至原大小的1.5倍,并被螺栓固定在模具上(如下图),纺织物上喷涂的刻度有助于确保拉伸的均匀。

3D材料选用肖氏硬度为45D的热塑性弹性体(TPE),因为该材料拥有良好的弹性。在预拉伸的纺织物上打印一个8边形,沿着红色的3D打印材料切割后,得到下右图的形状。

1.2 力学分析
我们可以分析得出整个形变过程,参与的材料和对应的力学行为可以简单地分为:
a. 布料 – 收缩
b. 3D打印材料 – 保持原有形状
2# 将主要的力学特征转换为Kangaroo的约束
在Kangaroo里面,每个电池都可视为“约束“。按照这个思路,上文提及的力学特征可以通过Kangaroo的约束来表达。
对于布料而言,它是简单的一个收缩的行为,因此是长度约束。可以用Kangaroo2-Goals_Mesh-EdgeLengths来模拟。
对于3D打印材料而言,它的长度几乎不会发生变化,因此也可以用

思考
为何会出现这种情况?不妨再观察模拟结果和真实物体之间的差别。可以发现,由3D打印材料附着布料的部分原本是光滑的,曲线十分平滑,而模拟网格的边缘却十分嶙峋。

解决方法
3D打印结束后,材料定型了,红色的线段是有韧性的,不容易产生右边这种皱褶。那么这种“平滑“可以被看作是网格最外层的边缘(naked-edge)相互之间的角度保持不变,即角度约束。结合它的长度约束,可统一用Kangaroo2-Goals_Angle-Rods来表达。
3# 搭建Kangaroo模拟系统
接下来用四步法来设计这个算法,即明确:
a.输入input
b.输出output
c.关键性步骤key process
d.中间步骤intermediate process
a.输入input ▶▷
输入是一个曲线(curve),该曲线是3D打印喷嘴的路径
b.输出output ▶▷
输出是一个网格,即发生形变后的物体
c.关键性步骤key process ▶▷
该步骤是通过Kangaroo2-Main-Solver来模拟
以上步骤可总结为下图:
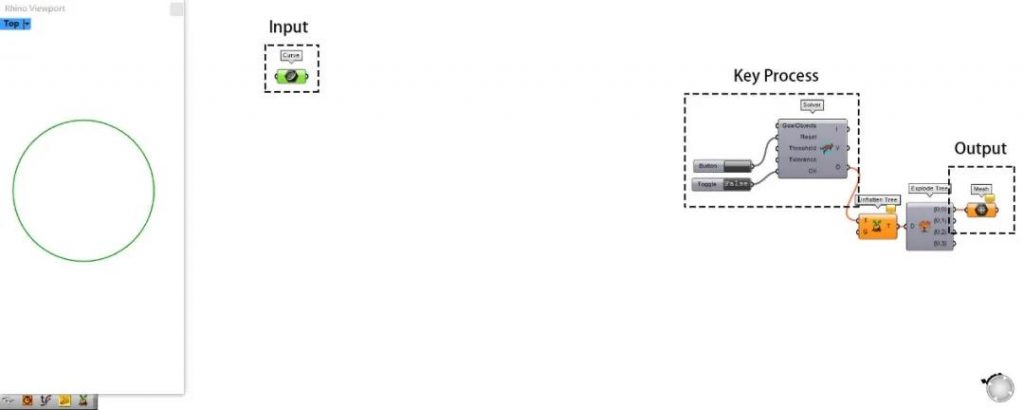
在理清大致的框架之后,可得知整个程序最重要的地方在于这个为Solver准备各种数据的中间步骤(intermediate process),然而需要哪些数据已经在前文提及。下面开始中间步骤:
d.1 将曲线Curve转换为网格Mesh ▶▷
纺织物是沿着3D打印喷嘴的路径切割获得的,因此3D打印喷嘴的路径形成的圆即为模拟的纺织物。因此这一步是将3D打印的路径(Crv)转化为网格,网格也是Kangaroo2模拟常见的数据结构。
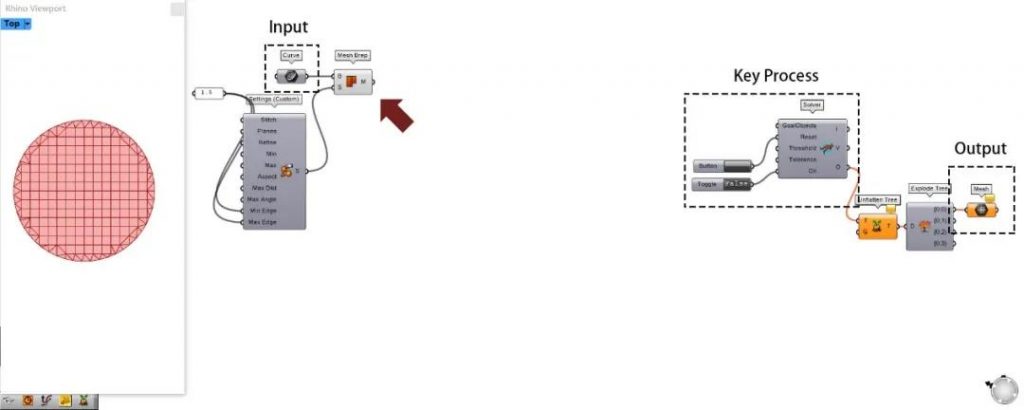
# 备注
Setting里面的长度为生成网格的目标边缘长度,可根据形状不同合理调整。
d.2 重构网格 ▶▷
观察上图左侧的网格结构,几乎为正方形结构。而在有限元分析(finite element analysis)里,常用的网格结构是各向同性(isotropic)的,原因是这种结构可简化线性弹性的模拟。该结构可通过Kangaroo2-Mesh-SimpleRemesh电池计算获得。
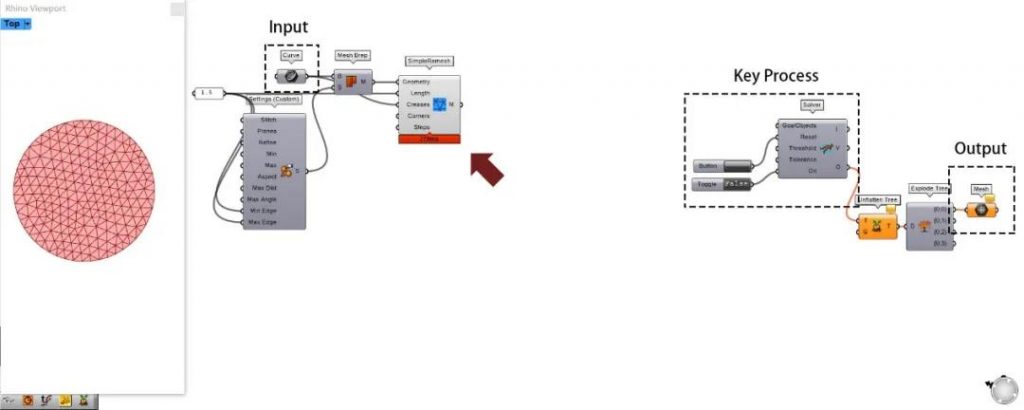
d.3 Kangaroo2-Main-Show ▶▷
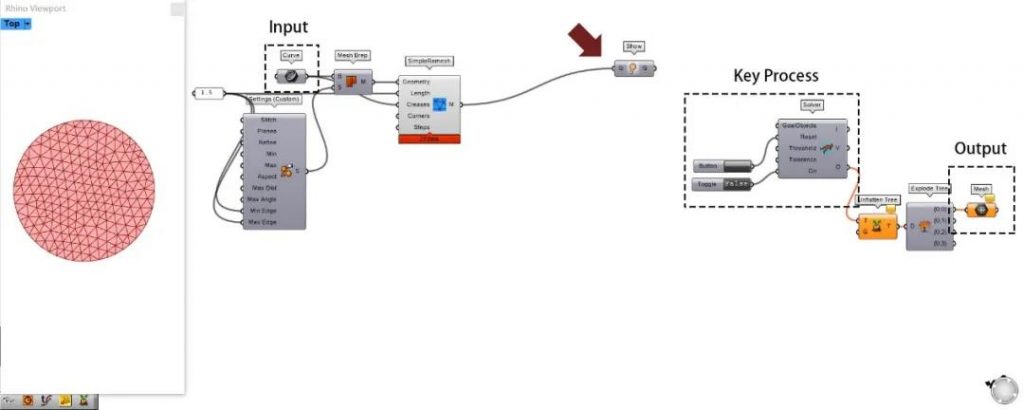
d.5 模拟3D打印材料的特性 ▶▷
上文提及模拟3D打印材料有2个约束,长度约束和角度约束。该步骤可细分为:
d.5.1提取代表3D打印材料的最外层网格边缘
d.5.2 把外层边缘连接成一条完整的曲线
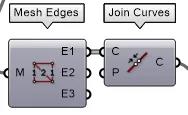
d.5.3 接入Kangaroo2-Goals_Angle-Rods电池
d.5.4 调节Axial Strength和Bend Strength参数大小
# 如何理解这两个力?
想象你手中有一根鼠标线,Axialstrength是沿着鼠标线方向拉扯受到的阻力,BendStrength是折弯鼠标线受到的阻力。在现实物理世界,前者是远远大于后者,这很好理解,你很难把你的鼠标线拉长,但是你可以很轻松把鼠标线卷起来。
LengthFactor和AngleFactor保持为1,即它们保持和初始一样的形态(犹如3D打印完成后它们不会发生变化)。
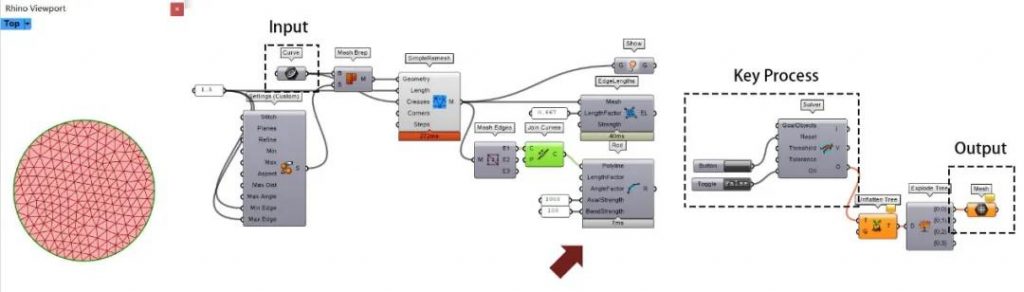
d.6 数据导入 ▶▷
最后用Entwine, Unflatten Tree和Explode Tree组织数据的输入和提取需要的数据。
# 注:不清楚这一步的朋友可以回看Kangaroo系统兴趣课程-01-01 k2 核心特性比较 案例01
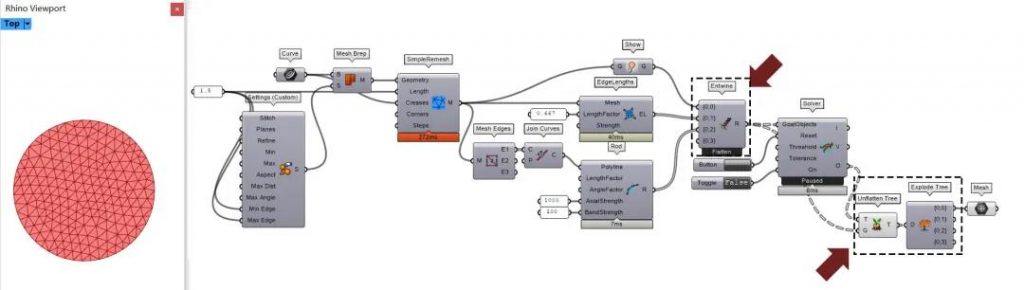
出现问题?
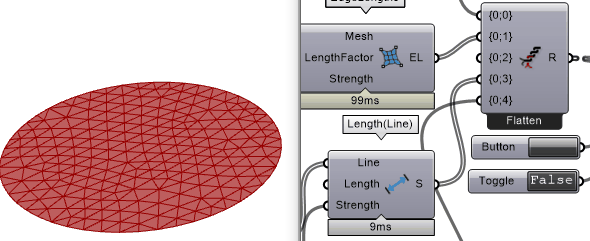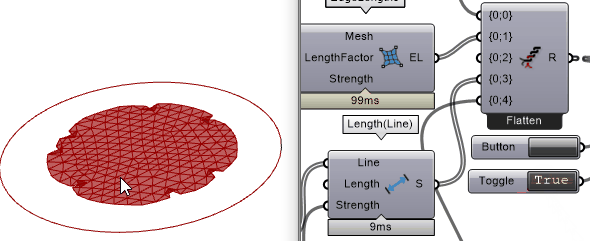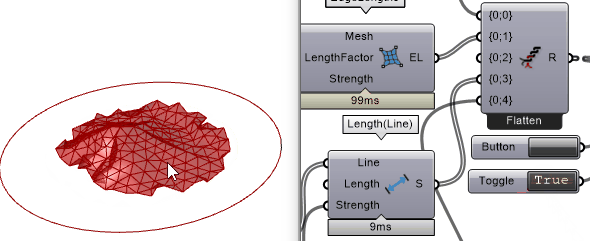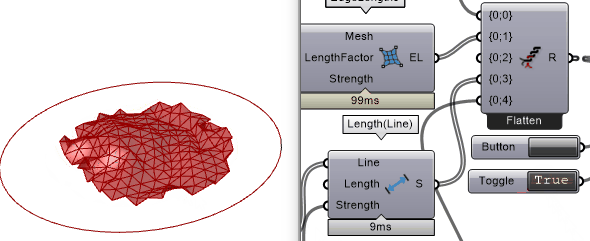
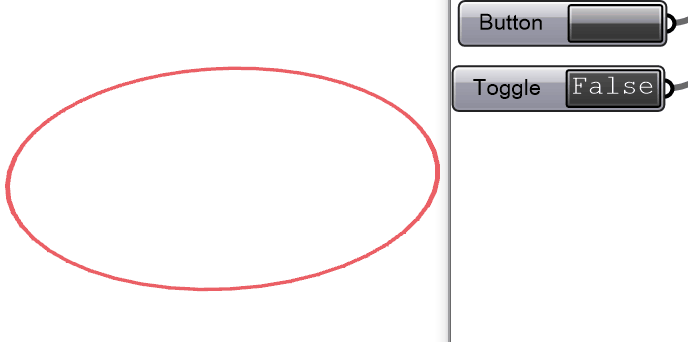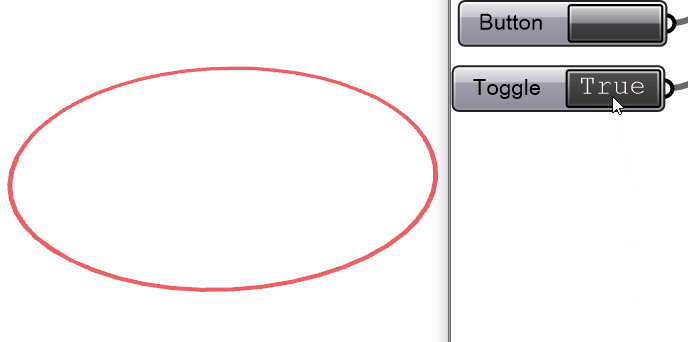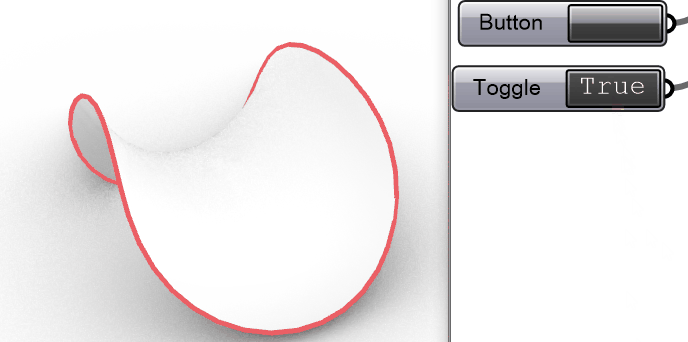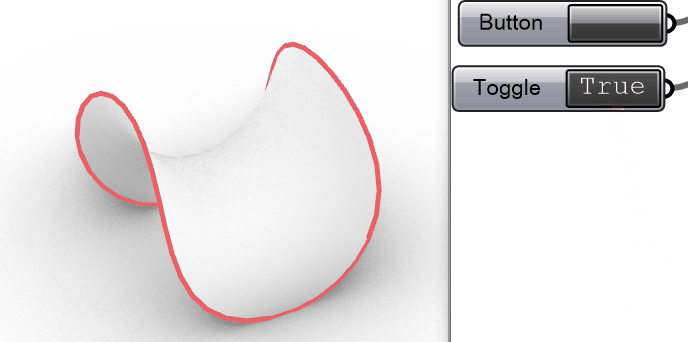
把Solver开关打开,开始模拟。此时网格收缩了,但是并没有出现x-y-z空间上的形变,只有x-y平面上的形变。为什么?
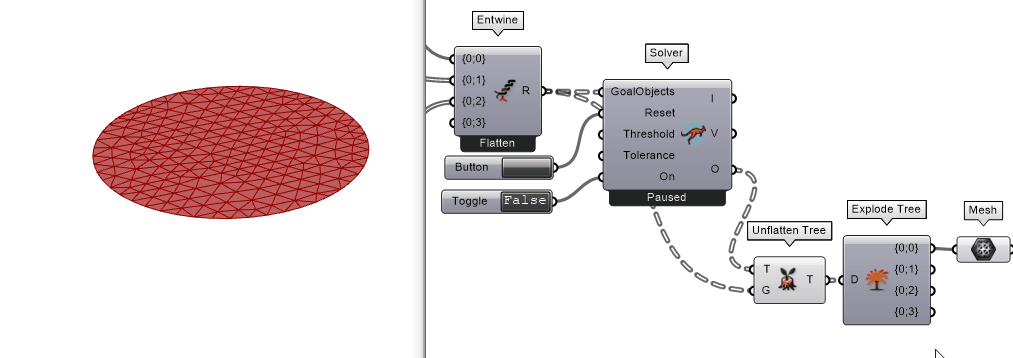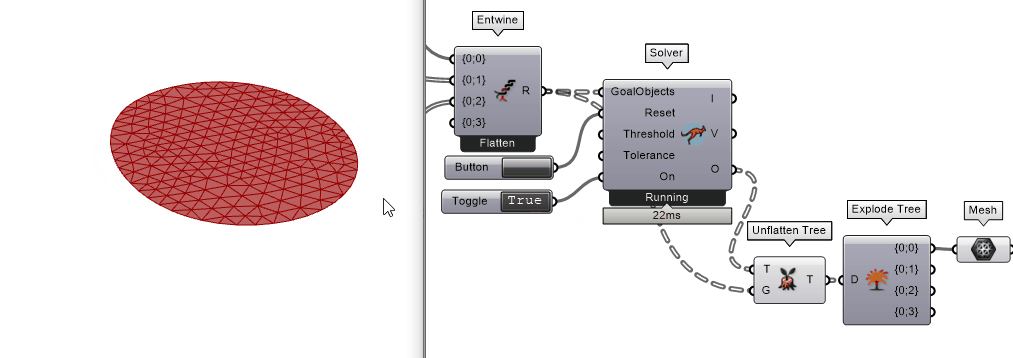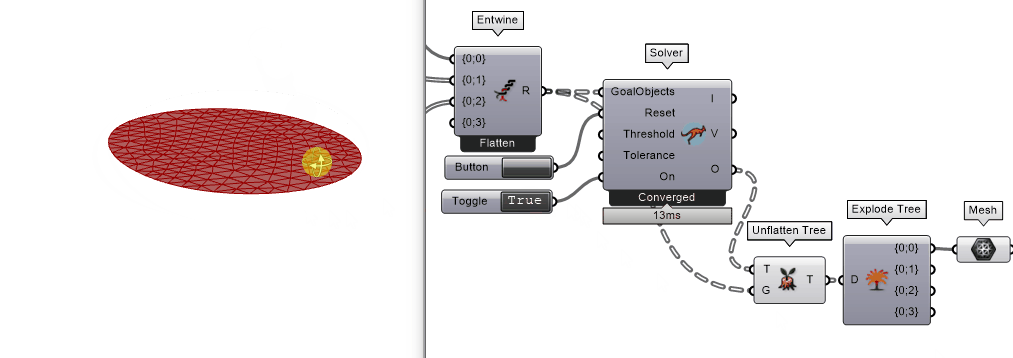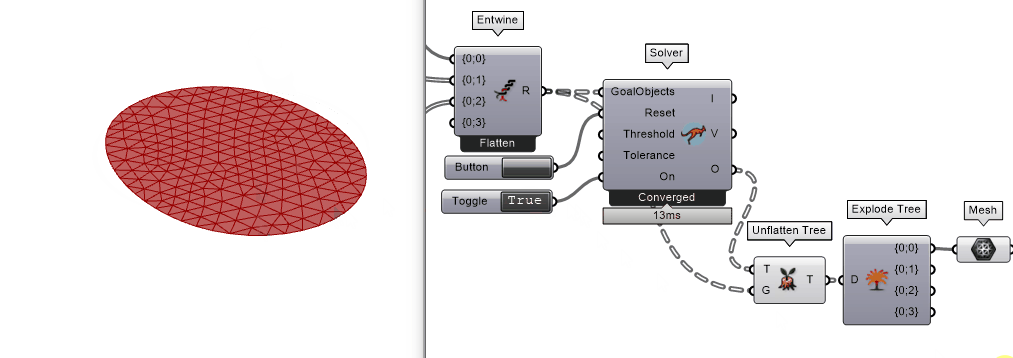
思考
网格由圆形变成椭圆,那说明整个模拟程序在起作用。没有发生z轴方向形变的原因是在电脑里面把纺织物收缩理想化在x-y平面,而在现实世界里,总有一些“随机的”因素来打破这个x-y平面的平衡。例如:切割的桌面不是水平的,切割的时候不小心碰到了材料而产生了z轴方向的力,等等。
解决方案
往这个系统添加打破平衡的力。
方法一 ▶▷
添加Kangaroo2-Main-Grab来手动拖拽打破平衡
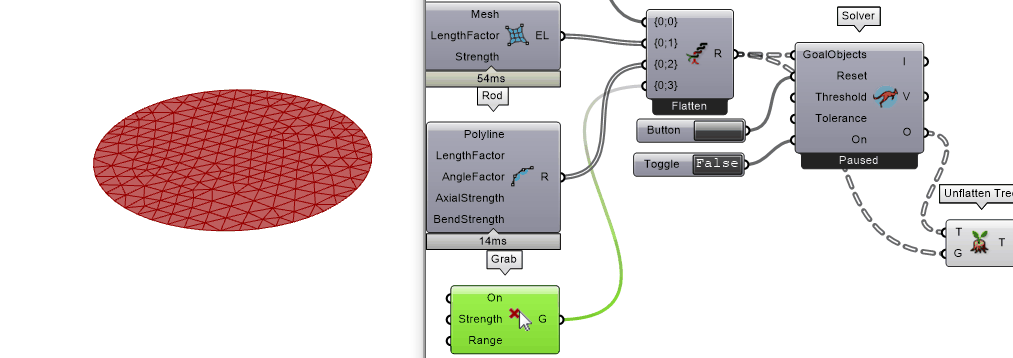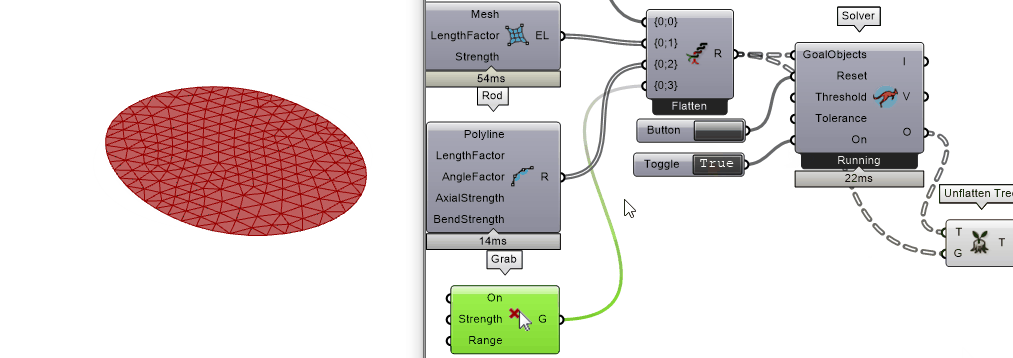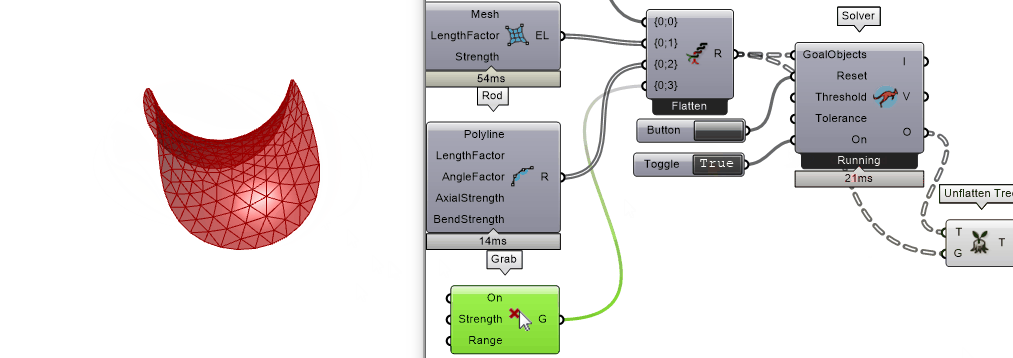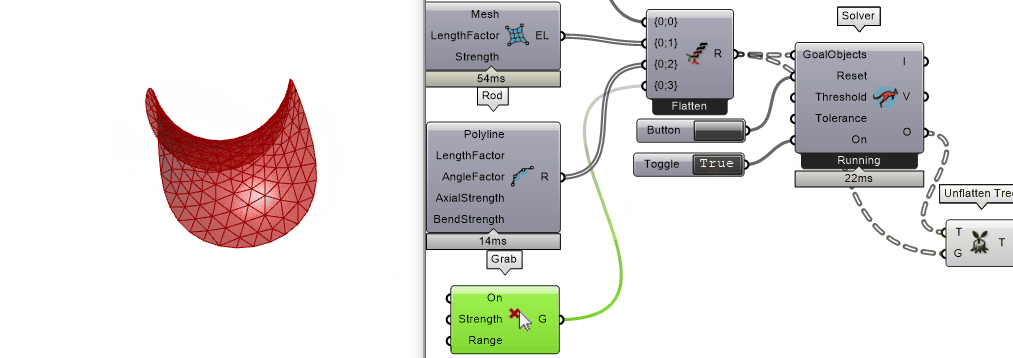
方法二 ▶▷
添加Kangaroo2-Goals_Points-Anchor
上述方法可打破平衡,但如果想实现“自动化”的话,这种方法并不可行。上述方法的本质是在模拟开始之后某个顶点(vertex)往z方向位移。如果按照这个思路,Anchor电池能很好地实现这个想法。该电池把电池P端的点在运算开始之后移动到电池的T端(target),因此可以把网格中心一个顶点往z轴移动到目标位置来达到打破平衡的目的。
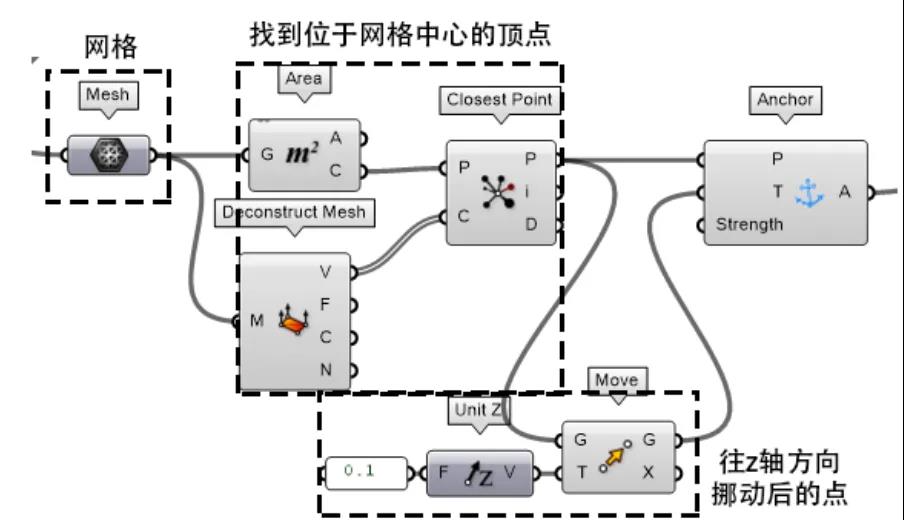
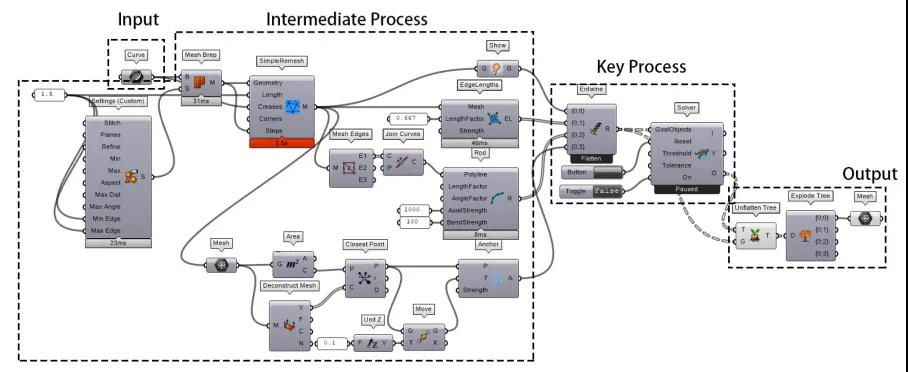
整个程序可以整理为:
调个色换个细腻的Artic显示模式之后,效果如下图:
4# 进阶模拟:一个程序解决所有3D打印路径
上文已经把用Kangaroo模拟这种形变的核心阐述了一遍,即角度约束和长度约束。而约束的对象是:
1.象征纺织物的网格(Mesh)
2.象征3D打印图案的网格边缘(Edges)
如果直接用上面的电池组是没法模拟一些复杂的3D打印路径的(如下图),因为上述方法用的是Naked Edge的方法得到最外层的裸露边缘。
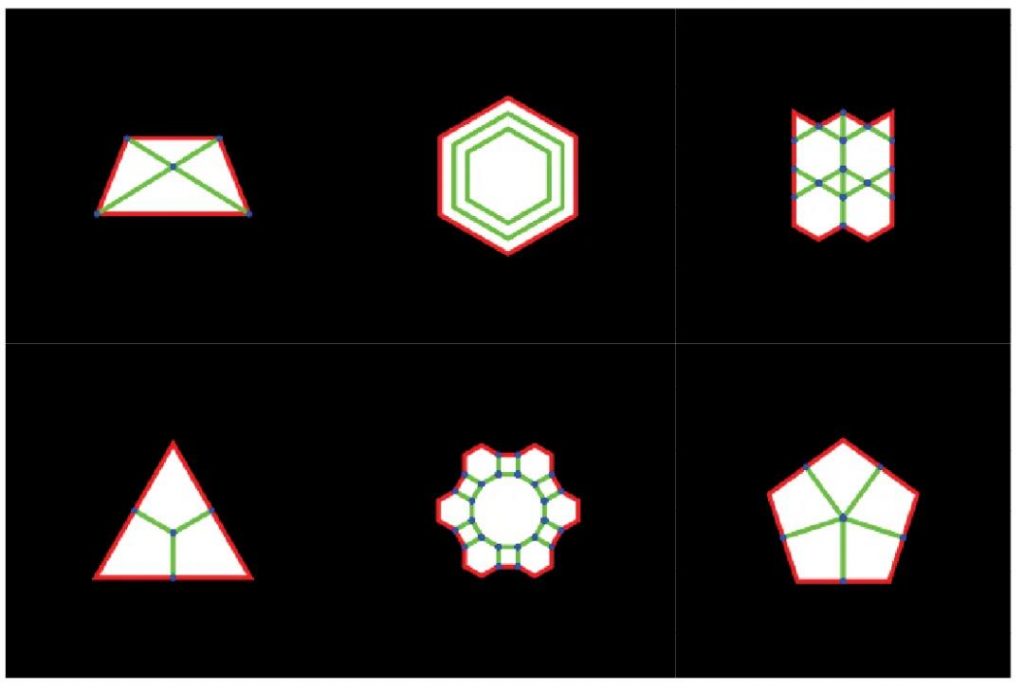
想要用一个.gh文件适用所有图案则需要一系列的几何数据处理,而这个过程的核心是
1. 保持生成的网格和原有的路径吻合
2. 在网格里面找到代表3D打印路径的网格边缘
按照这个思路,这个程序可以有以下7个部分:
第1步:提取外边缘形成曲面
第2步:提取内部边缘进行分割(若有)
第3步:均一化生成网格
第4步:重构网格
第5步:准备Kangaroo数据
第6步:Kangaroo模拟
第7步:输出网格模型

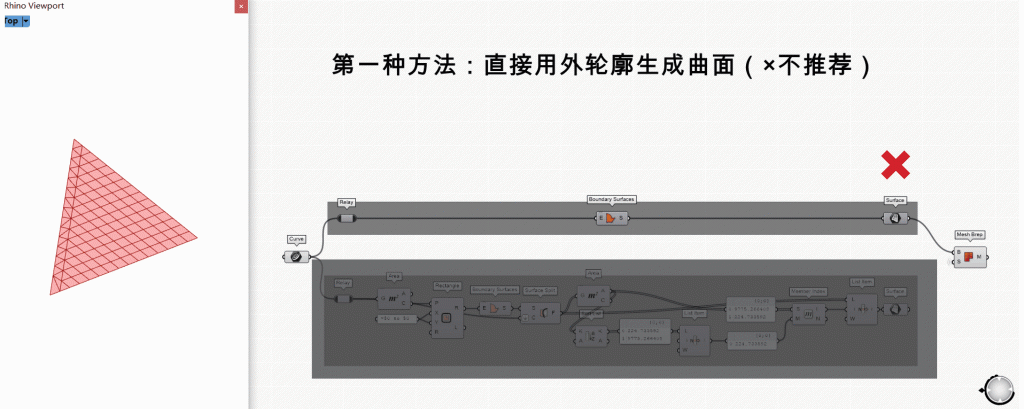
第1步:提取外边缘形成曲面 ▶▷
这一步可拆解为以下步骤:
1. 用BoundingBox创建包围盒[注意勾选UnionBox模式]
2. 将包围盒曲面向外偏移Offset
3. 将路径切割曲面SurfaceSplit
4. 删除0号曲面(最外层)CullIndex
5. 合并所有曲面BrepJoin
6. 提取最外边缘BrepEdges

第2步:提取内部边缘进行分割(若有)▶▷
这一步针对内部有轮廓的图案进行的操作(若没有内部轮廓程序也不会报错)。思路是先取所有线段的中点,若中点在第1步计算得到的外边缘上,则删除该线段,剩余的就是内部的线段了。判断点是否在线段上的方法有可以想到以下解决方案:
1. 计算线段中点到外边缘的距离,若距离=0则判定在线段上 (看似可行,但该方法是错误的)。因为计算距离是浮点数,并不能进行Equality操作,详细解释请看这里
2. 用PointInCurve电池,若R端输出为1,则判定在线段上。
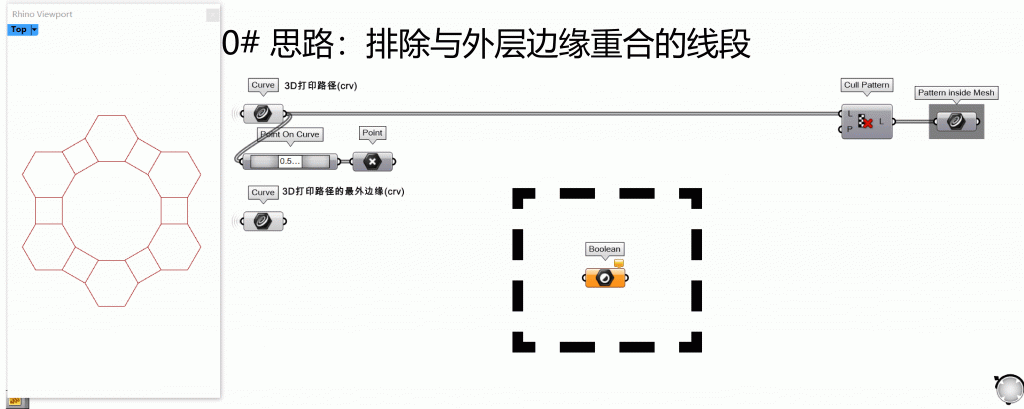
第3步:均一化生成网格 ▶▷
为了使所有由外边缘生成的曲面内部结构一致,这里要对所有形状均一化生成曲面。如果不做这一步操作,曲面的结构会不一致,这样也会导致后面的网格不一致。因此这一步的思路是:
1. 以图案中心建立一个uv和x-y平面一致且面积远大于外轮廓的正方形
2. 用外轮廓去切该正方形曲面SurfaceSplit
3. 通过面积排序筛选得到切好的外轮廓曲面
不同结构的区别具体请看下图,这里取三角形的曲面结构作对比,区别尤为明显。
曲面的结构是非常重要的概念,在Rhino原厂的课程多处提及。有疑惑的朋友可以复习Rhino原厂GH教程GH_02_15_Surface:
(若有内部图案)接下来用第2步得到的内部3D打印路径来切割上一步得到的曲面,再将分割好的小曲面转化为网格,最后将所有小的网格拼凑成一张网格即可。为何这里要用内部的图案去切割曲面?因为这样生成的网格的边缘能与3D打印路径契合,为下一步做准备。
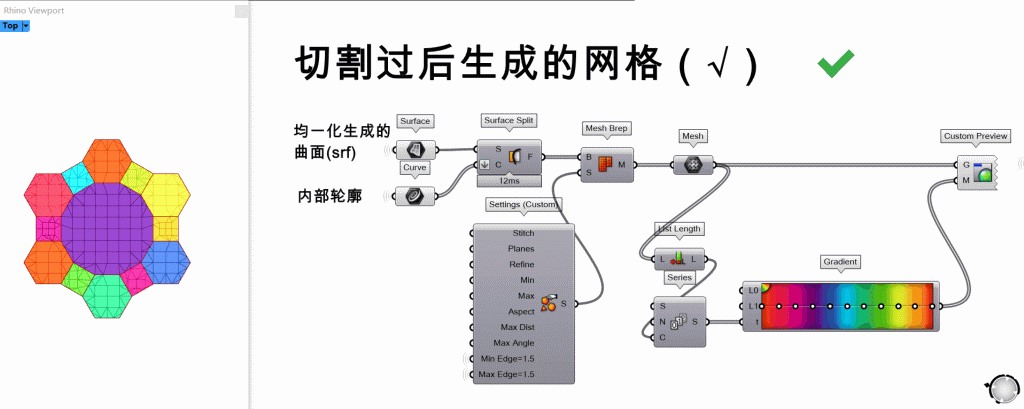
第4步:重构网格 ▶▷
上文提及的SimpleRemesh很容易出bug,所以这里改用一个能达到类似效果并且运算较快和少bug的电池-RemeshByColor。思路是:
1. 将第3步获得的所有网格碎块组合成整块网格MeshJoin
2. 提取第3步的网格碎块的所有裸露边缘MeshEdges
3. 通过提取它们的中点来判断是否重合,用到电池PolygonCenter,CullDuplicate
4. 提取这些边缘的起始点,并将重合的删除CullDuplicate
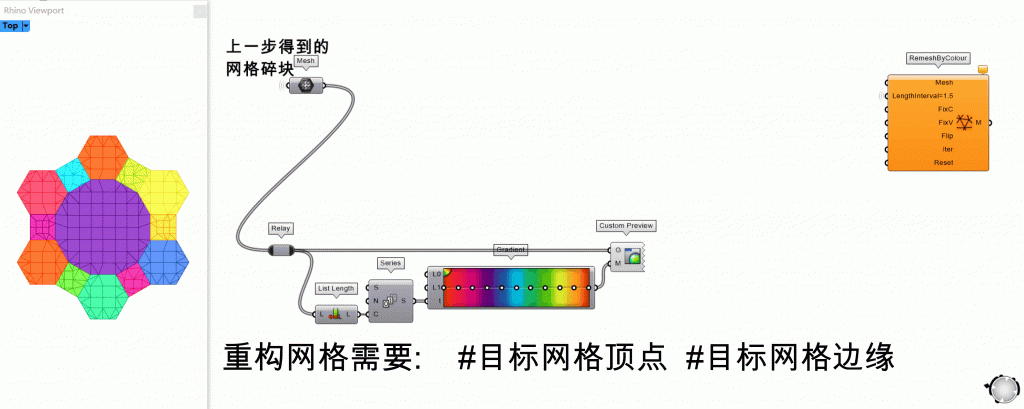
第5步:准备Kangaroo数据 ▶▷
两个需要得到的数据,一是网格本身(这个已经有了,直接连接即可),二是代表3D打印路径的网格边缘,即有角度约束的线段。思路是:
1. 将第4步获得的网格碎块的外边缘偏移形成矩形区域
2. 提取第4步的MeshJoin后的完整网格的所有边缘的中点
3. 通过判定中点是否在矩形区域内PointInCurves电池的R端=2(inside),来筛选完整网格里面代表3D打印路径的网格边缘
如下图,洋红色的矩形区域(1.),红色的是中点(2.),青绿色是(3.)筛选得到的边缘。
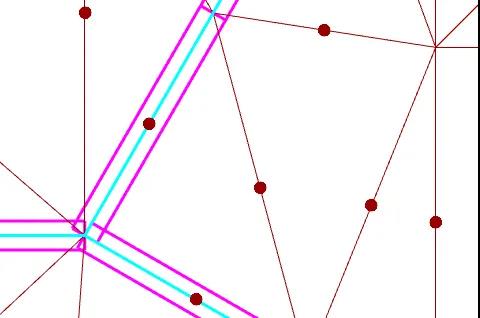
对于步骤(1.)偏移生成矩形区域这一步,推荐使用GH插件PufferFish的双向偏移,也可用笔者做的简易版。
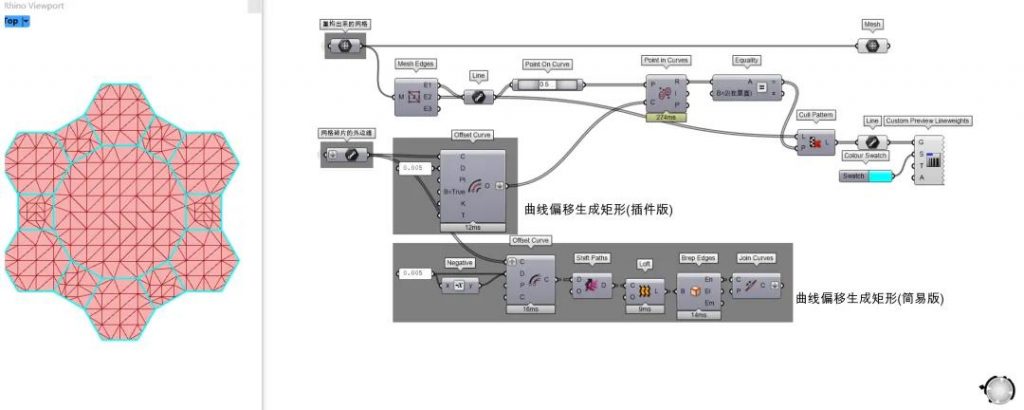
第6步:Kangaroo模拟▶▷
这一步核心是解决角度约束问题,之前的模拟将角度约束和长度约束一并使用Rods电池来实现。虽然这个十分方便,但是它只能运算两条边之间的角度约束。如下图的图案,交点可能是三条边甚至更多,因此Rods没法解决这种情况。
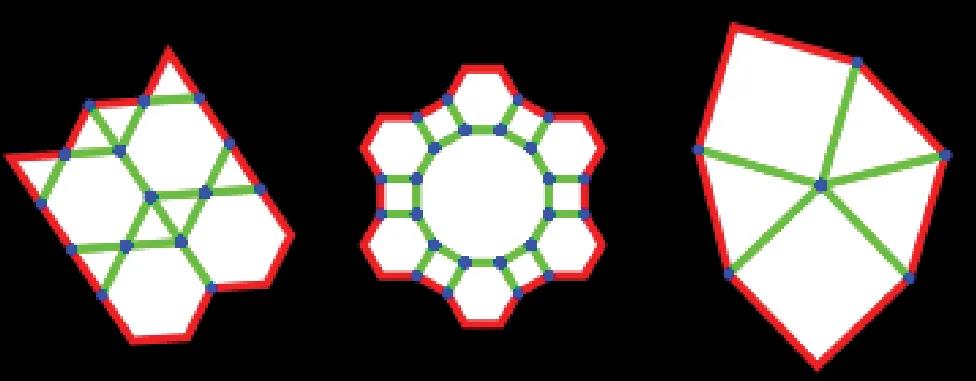
出现问题?
那如何解决这种三条边相交形成的角度约束问题呢?
思考
角度约束的本质是两两计算的,它输入的本质是Kangaroo2-Goals_Angle-Angle的LineA和LineB。如果把所有相交的线段以两两相交的形式输入是不是就可以解决?(角度约束具体原理可复习Kangaroo课程/3-1
解决方法
GH里正好有一个叫Intersection-Physical-MultipleCurves的电池,它可以找到凡是相交的线段,以两两相交的形式输出。
将第5步整理好的数据接入,完整的Kangaroo参数如下
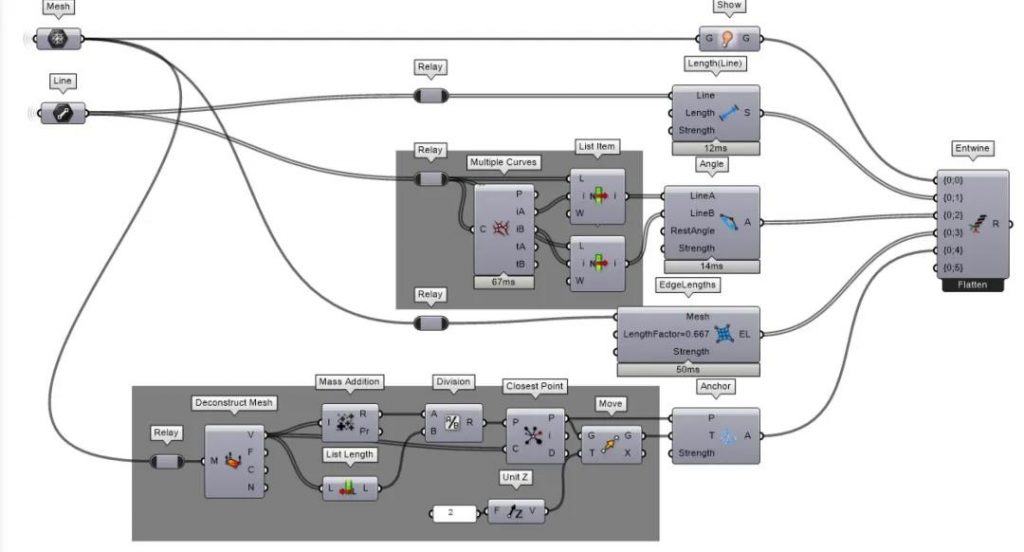
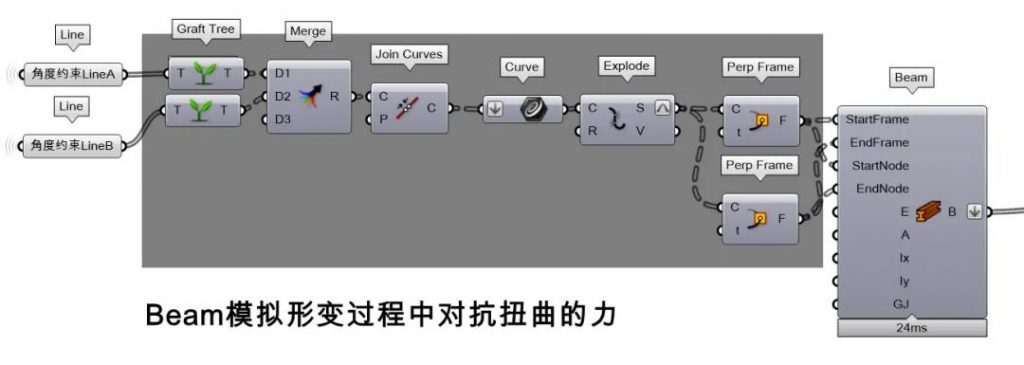
剩下的就是调节参数以求达到接近真实的形态,可以手动调参或者使用优化算法。笔者在论文里面用了后者,通过3D扫描获取真实的3D打印样本的网格数据以作ground-truth object,再通过三维重建的目标函数来优化Kangaroo的参数。这里只提供思路,涵括的内容不在本文内。
第7步:输出网格模型 ▶▷
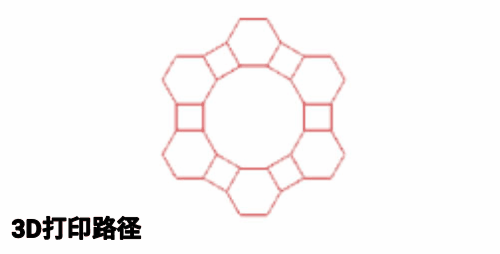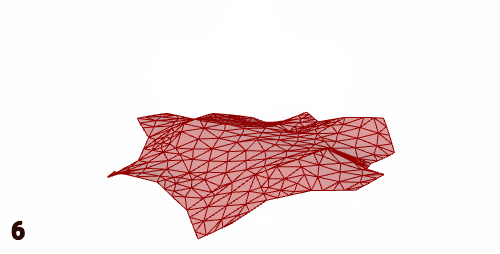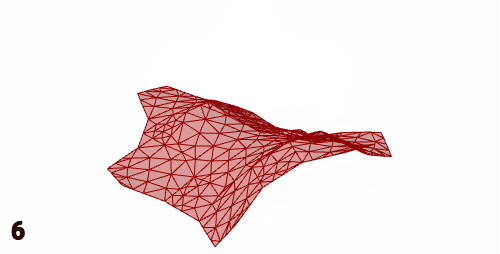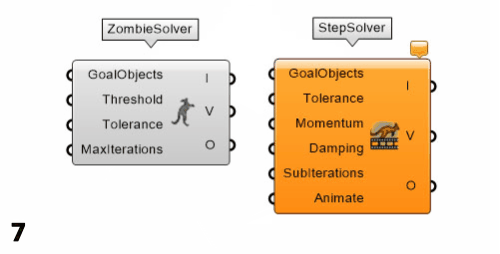
日常使用的Solver和BouncySolver有助于观察形体的变化,但是它却不能很好地实现自动化这一目的。在满意参数的情况下,如果想自动导出模拟好的网格,可以通过以下两个电池来实现:ZombieSolver和StepSolver。
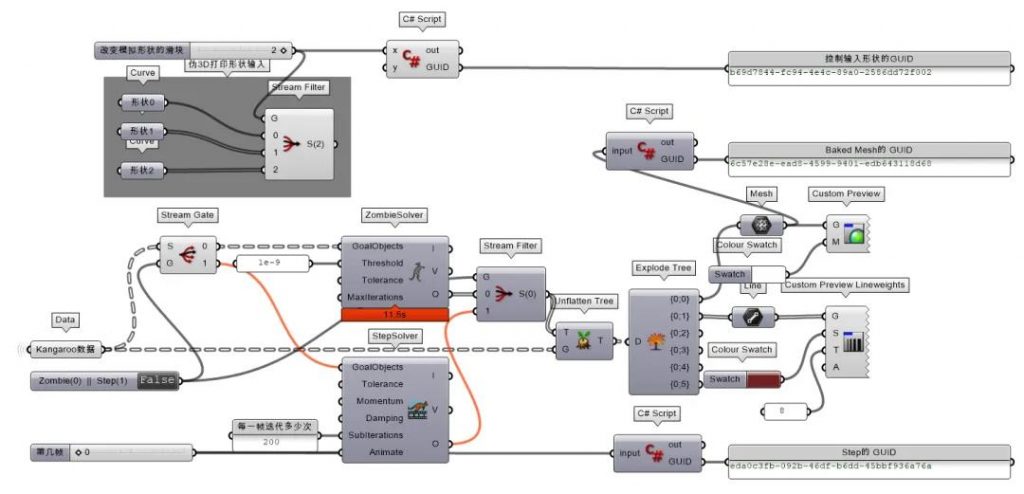
ZombieSolver:
这个电池非常适合自动化工作流,因为它不需要像Solver那样需要手动开关,而且每次更换输入也不需要Reset。有两个参数值得注意,它们都是在精度和时间两者之间做取舍的参数。
-
Threshold. 控制模拟运算的精度,默认是1e-10
-
MaxIteration. 控制模拟运算迭代的次数,默认是5万次
笔者这里提供一个结合Rhino的PythonScript自动导出网格的工作流。假设你用滑块(NumberSlider)来迭代输入的形状的序号(index),这里简化用StreamFilter演示,那么可以:
-
新建一个C#电池,把右边的A端改成GUID
-
把以下代码粘贴进去获得NumberSlider的GUID
List<Guid> guids = new List<Guid>();
foreach (Grasshopper.Kernel.IGH_Param param in Component.Params.Input)
{
foreach(IGH_Param source in param.Sources)
{
guids.Add(source.InstanceGuid);
}
}
GUID = guids;
3. 获取滑块和要bake的网格的GUID
4. 在Rhino窗口-Tools-PythonScript,输入以下代码,需要更改的参数以#井号在后面注释。
import rhinoscriptsyntax as rs
import Rhino
gh = Rhino.RhinoApp.GetPlugInObject("Grasshopper")
rs.EnableRedraw(True)
workingDir = rs.BrowseForFolder(None, "Select Working Directory")
rs.WorkingFolder(workingDir)
num_pattern = 3 #your max_num of slider
for i in range(0,num_pattern,1):
gh.SetSliderValue("b69d7844-fc94-4e4c-89a0-2586dd72f002",i)#GUID, number slider
gh.RunSolver("210201_Main.gh")#your gh file name
baked = gh.BakeDataInObject("6c57e28e-ead8-4599-9401-edb643118d68")#GUID, mesh
filename = str(i) + ".ply"
rs.Command("_SelNone", True)
rs.Command("_SelLast", True)
rs.Command("_-Export " + filename + " _Enter" + " _Enter", True)
rs.Command("_Delete", True)
rs.Command("_SelNone", True)
StepSolver:
若是想做类似动画的效果,或者导出形变过程的网格(如下图),这个电池非常适合。


本篇分享到这里结束,希望大家能有所收获!

 Rhino 原厂面授课程
Rhino 原厂面授课程



 在线录播课程
在线录播课程